A prime number is a positive integer that can only be exactly divided by itself and 1.
Algorithm: to judge whether X is a prime number or not, we can assume a number n has n x n = X (n = sqrt(X)). If X is not prime, it will have at least one integer pair n1 and n2, such that n1 x n2 = X, n1∈[2,n], n2∈[n,X]. We can then narrow down the scope that if X is exactly divisible by a number between 2 and sqrt(X), it is not a prime; otherwise, it is a prime.
sqrt(2021) ≈ 44
If we divide 2021 by integer between 2-44 one by one, we find 2021 ÷ 43 = 47. Therefore, 2021 is not a prime.
We can further refine the algorithm: X is exactly divisible by any prime number n1, n1∈[2,n]. Because all non prime numbers are ultimately divisible by some prime numbers smaller than itself.
In the case of 2021, we can try whether it is divisible by 14 prime numbers only rather than all 43 numbers between 2 and 44..
prime numbers between 2-44:
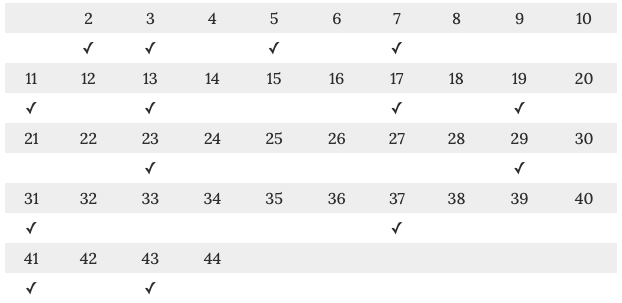
Alternatively, we can let the computer do the work:
def isPrime(num):
# Invalid numbers
if num<=1 or num!=int(num): return False
# narrow down: numbers divisible by 2 or 3
if num>3:
if num%6!=1 and num%6!=5:
return False
# divide num by numbers between 2 and sqrt(num)
sqrt=int(pow(num, 0.5))
for i in range(2, sqrt+1):
if num%i==0:
return False
return True
print(isPrime(2021))